Zero-Knowledge Proofs and the Pursuit of Trustless Transactions

General ramblings on zero-knowledge proofs, zk-SNARKs vs. zk-STARKs, and the path towards the blockchain's original promise of privacy.

Ali Baba’s Cave

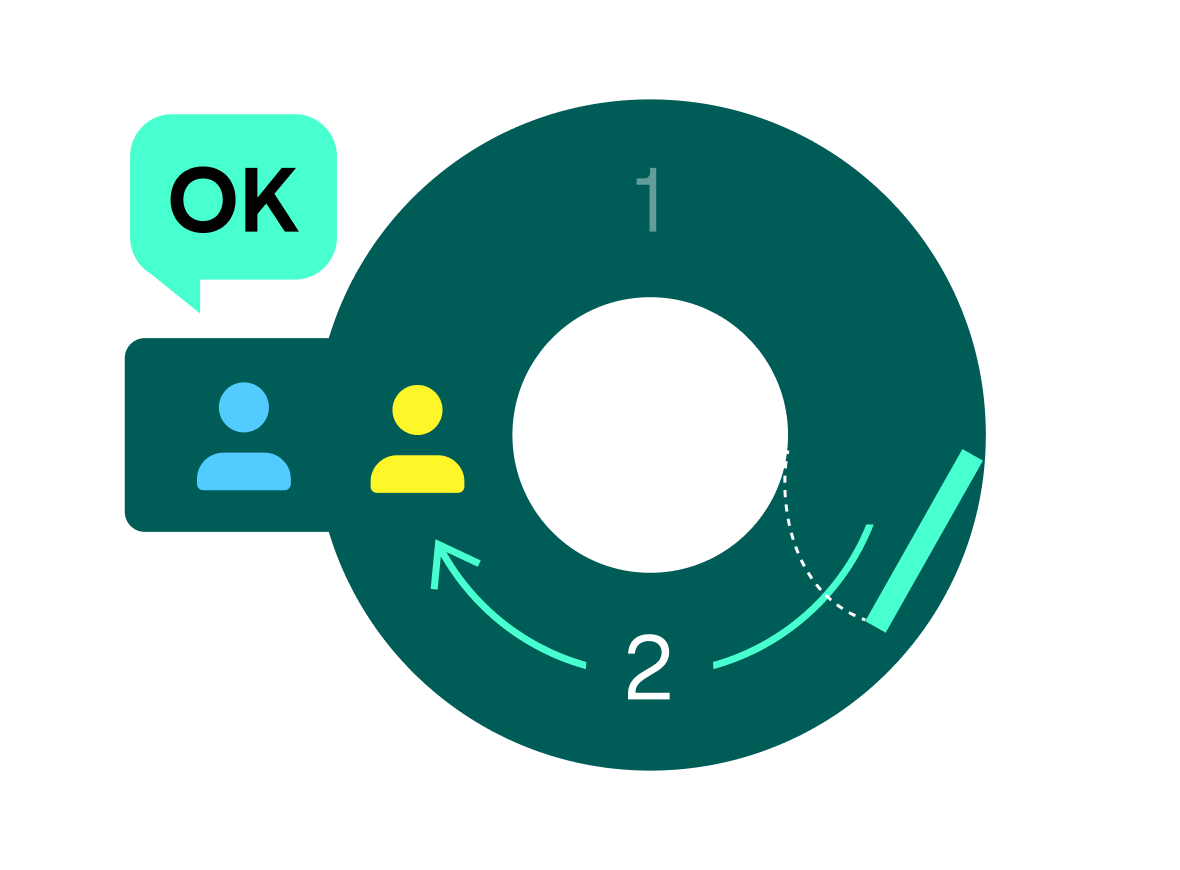
Let’s imagine a ring-shaped cave with a single entry and a magical doorway that separates two distinct paths. In order to go through the magic doorway, one must say a secret word aloud, which unlocks the doorway and allows the individual to walk through it. 

Bob (blue) wants to verify that Alice (yellow) knows the secret word, and Alice wants to ensure the word remains a secret—but prove to Bob that she knows it. In order to do this, Bob agrees to wait outside of the cave, while Alice enters and walks to the doorway separating the two paths.

Bob then walks by the entrance and shouts which side he wants Alice to appear from. Bob yells: “Path 2!”

If Alice truly knows the secret word, she will reliably show up from the path Bob names. The whole process must be repeated several times to ensure that Alice is not choosing the correct path by luck. Bob never learns of the secret word, but can verify with certainty that Alice knows it simply by observing her actions.

Alice and Bob have just displayed a zero-knowledge proof—an essential tool in modern cryptography, allowing two parties to interact with one another while still maintaining their privacy and security.

Zero-knowledge proofs are used in a wide range of applications, including password verification and identity validation, to demonstrate knowledge without revealing any confidential information to an outside party. As new threats emerge and privacy concerns continue to rise, the development and implementation of advanced cryptographic techniques such as zero-knowledge proofs will remain crucial in safeguarding our online interactions and protecting sensitive information.

So, now that we’ve graduated from An Introduction to Zero-Knowledge Proofs, led by Professors Alice and Bob. It’s now time to venture further out of the cave, where we’ll explore some more advanced zero-knowledge applications. But first, some important zero-knowledge acronym breakdowns:

zk-SNARK = Zero-Knowledge Succinct Non-interactive Argument of Knowledge
zk-STARK = Zero-Knowledge Scalable Transparent Arguments of Knowledge

Here we go.

Why are zk-STARKs fully trustless and zk-SNARKs not?

zk-SNARKs require what is known as a trusted setup, which refers to the initial creation event of the keys, which are used to create the proofs required for private transactions and the verification of those proofs. When these keys are created, there lies a hidden parameter linked between the verification key and the keys sending private transactions. So, if the secrets used to create these keys are not properly destroyed, they could be utilized to forge transactions by false verifications, since these secrets form the basis for all subsequent trustless transactions. This would entirely undermine the system, rendering it completely meaningless. If this scenario were to occur, a bad actor could theoretically create new tokens out of thin air, for example. This initial creation “ceremony” is a major point of contention in the debate of zk-SNARKs vs zk-STARKs and is the most profound single point of failure for zk-SNARKs.

zk-SNARKs have a quantum issue

zk-SNARKs just can’t seem to catch a break. There is significant debate on whether or not there is a backdoor into elliptic curve random number generators, upon which zk-SNARKs are entirely based. Currently, the algorithm remains generally secure, but vulnerabilities via side-channel attacks do exist—although these can be mitigated by some simple design mechanisms. The larger threat to zk-SNARKS comes from the not-so-distant reality of the proliferation of quantum computing. There is a chance that quantum computers will be able to successfully break elliptic curve random number generators and essentially unravel all the current cryptography that all cryptocurrencies are modeled on, which is merely a consequence of Moore’s Law. Obviously, if this were to happen, there would be much bigger problems than the legitimacy of zk-SNARKs as fully secure zero-knowledge proofs.

zk-STARKs for the future—for the win!

On the other hand, zk-STARKs take an entirely different approach to zero-knowledge proofs  than their SNARK counterparts—one that is quantum-resistant and does not require any creation ceremony whatsoever. There is no potential for the proof to be corrupted by bad actors, and no “secrets” that need to be properly destroyed. Rather, zk-STARKs rely on hash functions. zk-STARKs are an argument of a knowledge system for an NP-complete computational integrity relation which satisfies the following properties:

• Zero-knowledge—proving possession of knowledge without revealing the specific information of that knowledge. If a statement is true, a verifier only learns that the statement is true and nothing more about the contents of the statement.

• Non-interactivity—not involving or requiring the actions or input of a user.

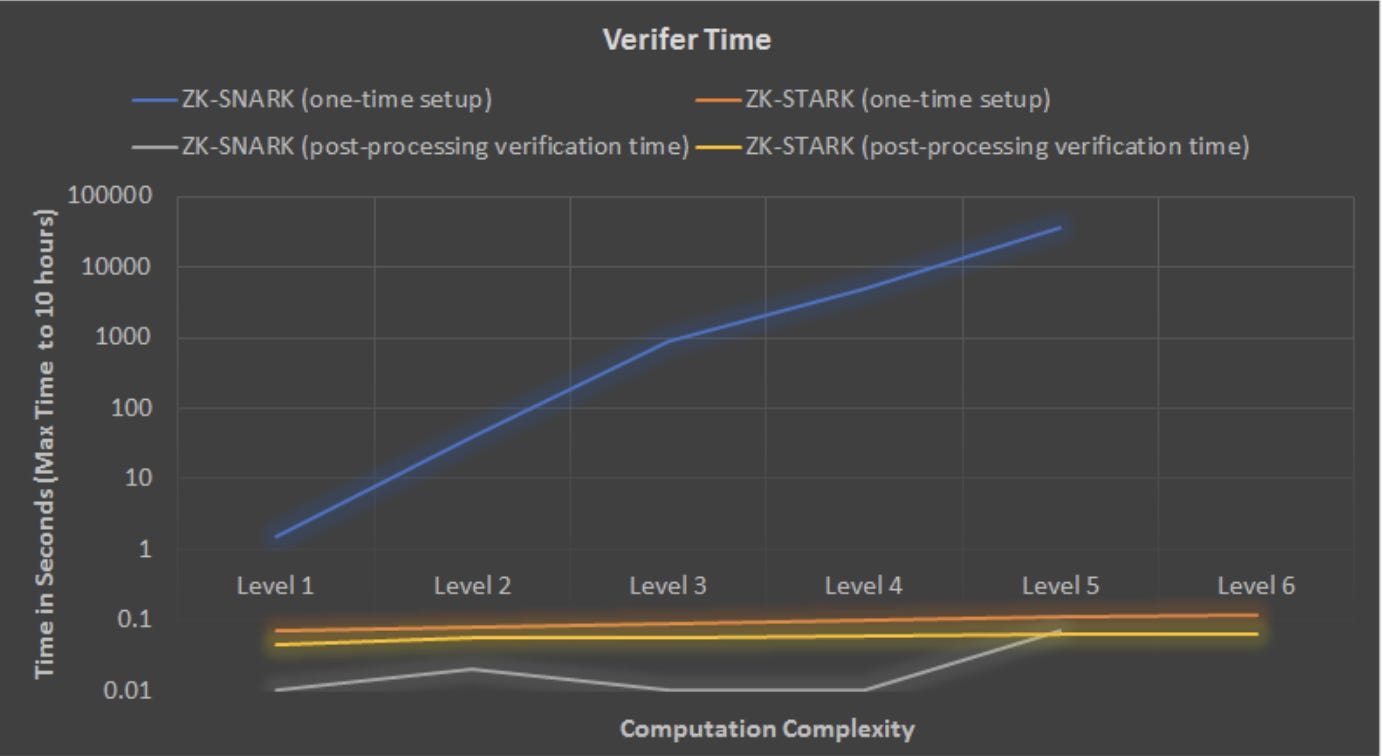
• Asymptomatically optimal efficiency—polylogarithmic proof size and verifier time, and quasilinear prover time.

• Transparency—all randomness in the setup is public and utilizes an interactive oracle proof (IOP), as defined below.

Essentially, if an interactive argument system were to be constructed, the verifier would be granted the freedom to probabilistically query the prover’s messages rather than reading them in their entirety. This type of protocol is called an interactive oracle proof (IOP). If all the verifier’s queries are generated from a uniform distribution, then an IOP can be made non-interactive using the Fiat-Shamir heuristic. In case you don’t know who Fiat and Shamir are, they are two dudes (Amos Fiat and Adi Shamir) who back in 1986 came up with this little idea of taking an interactive proof-of-knowledge and creating a digital signature based on it—so that some fact could be publicly proven without revealing the underlying information.

Hmmm… sound familiar? Some suggest Satoshi Nakamoto’s name is an anagram of their names together, but I digress…

To summarize a bit, the main innovation of zk-STARKs is the reduction of the computational integrity to verify certain statements, and the construction of a very efficient IOP. 

Charts source can be found here.

Weaknesses of zk-STARKs

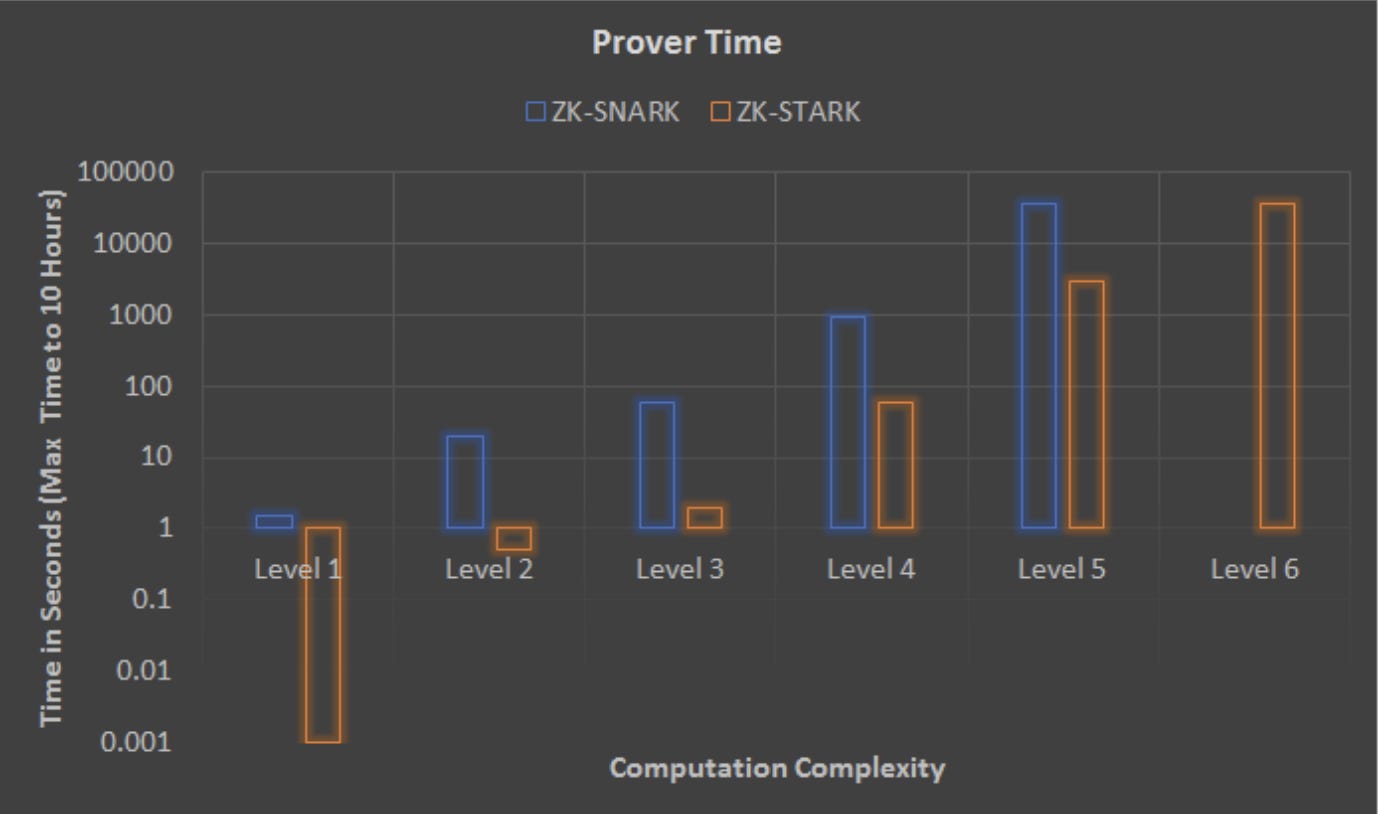
The only real issue with zk-STARKs is the fact that they are roughly 100x larger than zk-SNARKs. That said, I’d emphasize that their benefits far outweigh this size disparity, especially if you take a long-term view. More research is needed to mitigate this size issue by finding ways of shortening the proof length, or potentially aggregating or compressing several zk-STARKs using incrementally verifiable computation. However, there will always be tradeoffs between size and comprehensiveness.

There are also some concerns about the lack of documentation, research, and products that have been brought to market. zk-SNARKs were discovered before zk-STARKs, so they understandably have a major head start towards a full realization of their practice and implementation. There exist more products currently in use today that utilize zk-SNARKs—again, simply because they were made available much earlier than zk-STARKs. That, plus the thinner availability of developer documentation, combine to create some weakness regarding the proliferation of zk-STARKs. I expect this to change as time passes, and adoption of zK-STARKs grows.

Why does this all matter?

zk-STARKs have effectively been able to allow blockchains to move computations to a single off-chain zk-STARK provider, and then verify the integrity of those computations using an on-chain zk-STARK verifier. 

By utilizing zk-STARKs, a single “prover node” can, in quasilinear time, generate a proof that will convince all other nodes to accept the validity of its ledger—thus exponentially decreasing verification time. This is a far more efficient alternative to every node verifying every transaction, unnecessarily double-checking the current state of the ledger.